What is Quantum Computing?
September 3, 2018
Computers have revolutionized our world, touching almost every aspect of our daily lives. For this reason, the classical bit - the surprisingly powerful idea of storing information as either a 1 or 0 - occupies a position as one of the most fundamental advances in history. The fascinating realm of computer history is well worth diving into, as many have: the expansive Computer History Museum in Palo Alto, CA is a must-visit for enthusiasts, and Walter Isaacson's The Innovators is a fantastic chronicle of the journey to modern computing. As transformative their effects have been, there are still key problems that current computers simply can't tackle. Computer security experts will be familiar with the problem of finding the prime factors of very large numbers - the fact that classical computers can't do this efficiently is the basis for encryption. However, there are efficient algorithms for solving this and many other important problems using a quantum computer .

Quantum computing is a dynamic area at the intersection of physics and computer science. For an excellent introduction to the ideas of quantum computing, take the time to watch this talk by IBM's Dr. Talia Gershon. Most fundamentally, quantum information reformulates computation by allowing storage not in bits of merely a 1 or 0, but as qubits in superposition of 1 and 0. This almost certainly seems counterintuitive, and it is! Physicists have been arguing about the implications of quantum mechanics for decades. Exactly what is a superposition? After all, if you actually measure the qubit, you don't get back both 1 and 0 - half the time you will get a 1, and the other half you'll measure a 0. In physics, this is referred to as "collapsing the wavefunction". You might think, as some physicists have, that actually the qubit was a 1 or 0 the whole time; you just didn't know which until you measured it. Or perhaps more exotically, that every time you measured a 1, another parallel universe where you measured a 0 split off from this one! Although this theory sounds like science fiction, Caltech physicist Sean Carrol shared this blog post about why he considers the Many-worlds Interpretation the most likely one. The philosophical implications are of course ripe for exploration (this Stanford Philosophy article written by a physicist is a personal favorite), but for the rest of our discussion, we'll talk about superposition as a special state where we can't predict the outcome of measurement, only the probability.
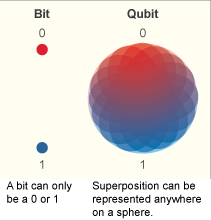
To begin to understand why superposition brings real advantages, we'll need to jump into the "spooky" world of entanglement. In quantum mechanics, it's possible to link separate qubits so that they aren't independent anymore. In the case of the "Controlled-NOT" operation, we entangle two qubits so that if you measure a 1 on the first qubit, the second one will "flip" (0 → 1 or 1 → 0). This may not seem very impressive, but it turns out to be quite powerful. We'll need to get a bit technical here, but reading things multiple times is a large part of physics!

Suppose we had a classical computer powered by just 2 bits. Each bit can be either one or zero, so we could have them both being the same (00 or 11) or them being different from one another (01 or 10). Remember, in a classical computer, each bit is completely independent of the others - no entanglement. Let's say we are doing a computation, and we want to change 00 into 11. How many steps does this take? We need to take the first 0 → 1, and the second 0 → 1, so two operations in total. Now let's return to our entangled qubits! If we want to change the quantum state, I only need to do one operation: change the first qubit. Let's see how this would play out:
- Start with the qubits in the 00 state
- Change the first qubit from 0 → 1
- Immediately, the second qubit sees that the first qubit is now a 1, so it has to flip from 0 → 1
- Now the qubits are in the state 11
We have essentially gone from 2 operations to 1, which doesn't really sound that impressive, but in fact, we could entangle an entire quantum computer. A classic 64-bit computer has 264 - 18,446,744,073,709,551,616 - bytes. While a classic computer can require up to more than 18 quintillion operations, a quantum computer can act on all qubits with 1 operation. A quantum computer however can represent them all at once via qubits. This ability to use all qubits as one is the key as it allows multiple qubits to interact with each other, with the net result being a process where the processes that lead to the solution we want reinforce each other while other bad solutions tend to cancel each other out.
What does all this quantum weirdness buy us? In addition to breaking RSA encryption, this extra computational power would also allow us to probe into the realm of chemistry, where limited computational power means that chemists must use many approximations to simulate even the simplest of molecules. Quantum computers would give us the ability to create new drugs and test exactly how they would interact with living tissues. There are also applications to AI, financial modeling, and even particle physics.
All this is very exciting; however, quantum computing is still a young field and faces some major challenges. Chief among these is fault tolerance. Quantum states are incredibly fragile and the slightest interaction with the environment will break them. The result is that qubits will become classical bits and all the extra states will disappear. In addition, quantum gates (like the CNOT) do not always perfectly entangle, which leads to more errors.
Scaling up in size while keeping your errors low is the major hurdle in building a practical quantum computer. Currently IBM leads the world with a 50 qubit computer, but others are jumping into quantum computing with gusto. Google is intensifying its efforts, and startups like Rigetti and IonQ are also contributing significantly to the exciting ecosystem of quantum computing.

Note that we haven't actually discussed how to actually build a quantum computer, and there are many different approaches! Superconducting qubits, ion traps, linear optical quantum computing, topological quantum computing, and more! Over the next few months, we'll be creating posts about each of these schemes, as well as information about events in the quantum computing industry. Lastly, we strongly encourage discussion, so please post any questions you might have about quantum computing in the comments below!